Tipi generici e relazioni di sottotipo

I generici non sono covarianti

Dati due tipi S $\prec$ T e due tipi generici G<T> $\prec$ H<T> può aver senso chiedersi quali delle seguenti relazioni covarianti di sottotipo sia valida

1. G<T> $\prec$ H<T>,
2. G<S> $\prec$ G<T>;

a titolo d'esempio, posto che Integer $\prec$ Number, ci si chiede cioè se

1. ArrayList<Number> $\prec$ List<Number>,
2. ArrayList<Integer> $\prec$ ArrayList<Number>.

Rispondere alla prima domanda è fondamentale per poter decidere che è legittimo l'assegnamento

List<Integer> li = new ArrayList<Integer>(List.of(1,2,3));

cosa che è già stata ampiamente sfruttata nella stesura del codice vista sino ad oggi e che, usando una immagine del tutorial, può essere rappresentata come

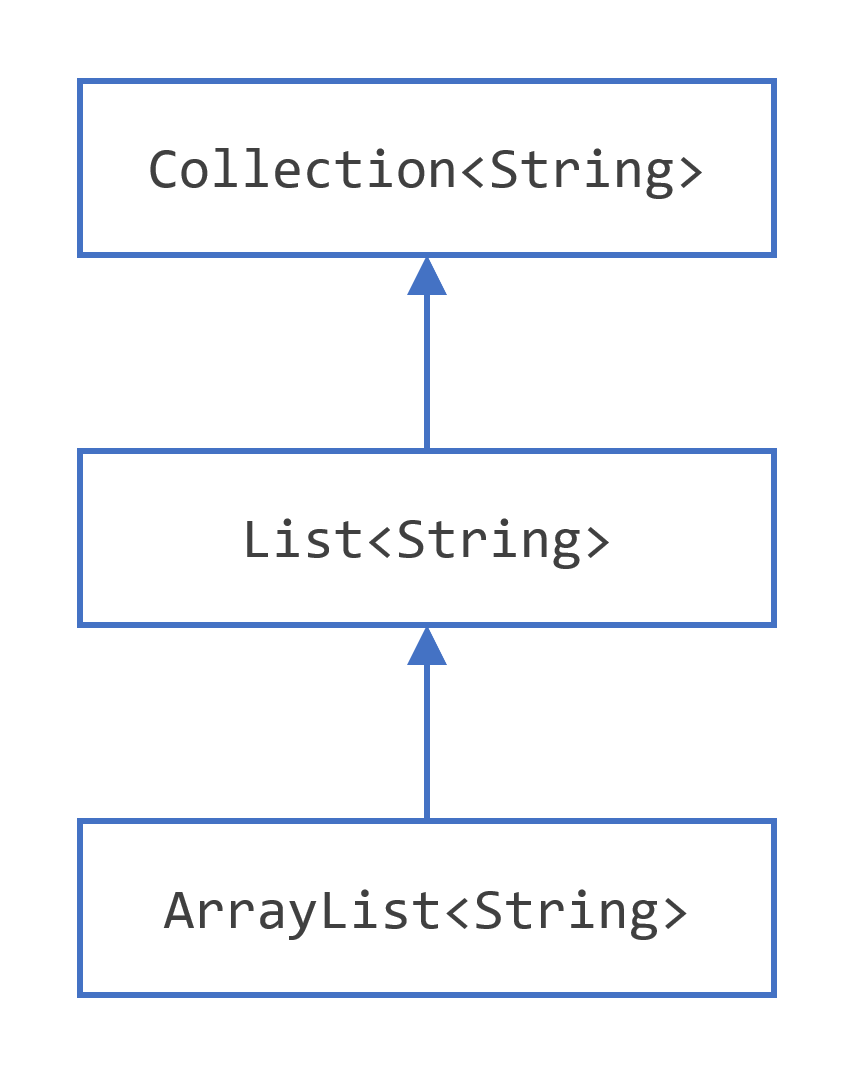
Rispondere alla seconda è necessario, ad esempio, per determinare se il metodo

double sum(List<Number> ln) {
  double sum = 0;
  for (Number n : ln) sum += n.doubleValue();
  return sum; 
}

può essere invocato non solo su argomenti di tipo List<Number>, ma per esempio anche su argomenti di tipo List<Integer>, come ad esempio li

sum(li);

|   sum(li);
incompatible types: java.util.List<java.lang.Integer> cannot be converted to java.util.List<java.lang.Number>

cosa che, come è evidente per via dell'errore riportato in precedenza, non è invece legittima; la questione può essere rappresentata come

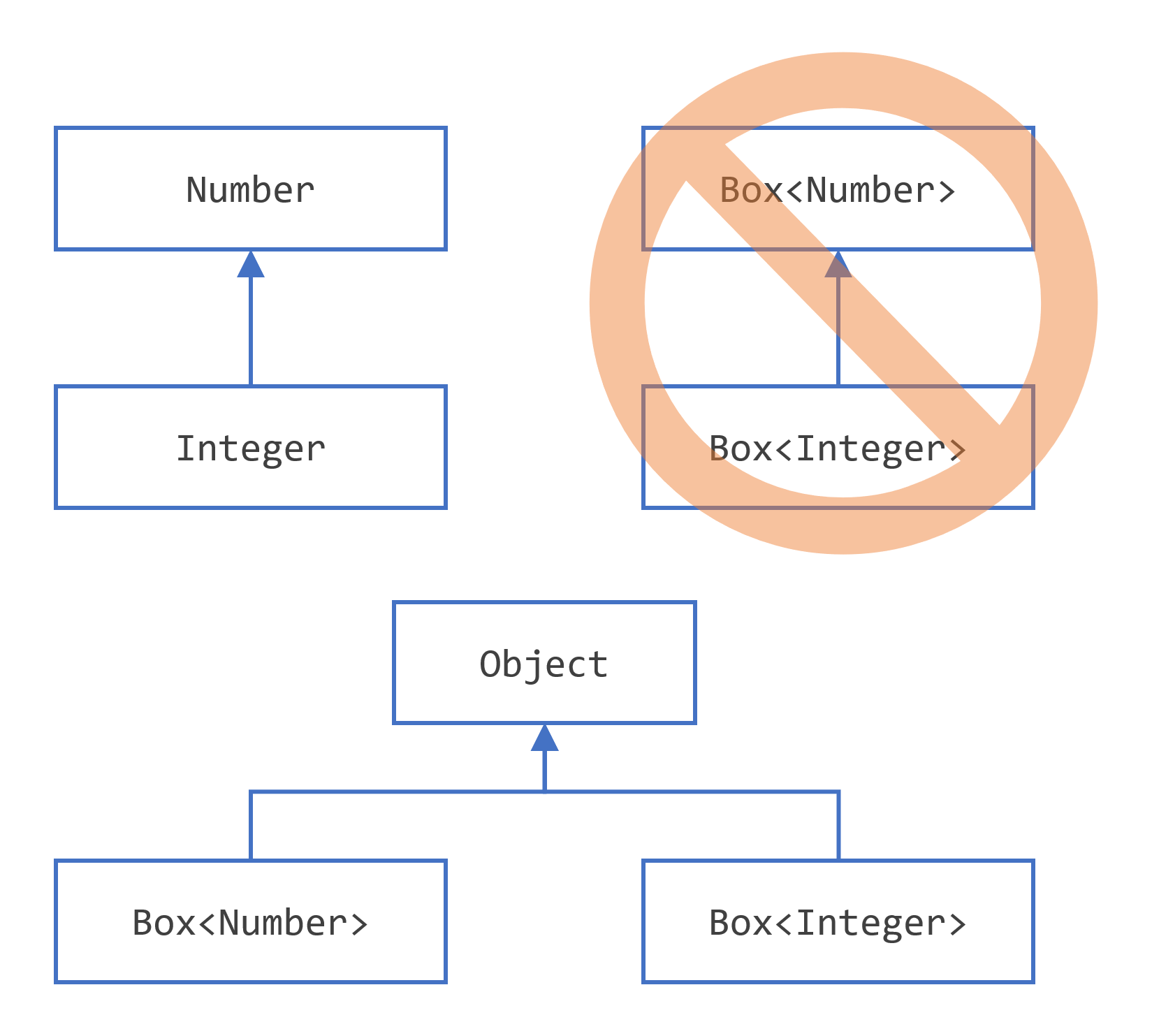
Perché i generici non sono covarianti?

Comprendere perché in genere non valga che G<S> $\prec$ G<T> anche se S $\prec$ T non è difficile. Immaginiamo che il seguente assegnamento sia possibile (senza il cast esplicito)

List<Number> ln = (List)li;

Una volta ottenuto l'alias ln potremmo usarlo per aggiungere a li anche dei Double

ln.add(2.5);

true

ma ovviamente, una volta estratto da li (come Integer) un Double darà adito ad un errore di conversione

li.get(3);

---------------------------------------------------------------------------
java.lang.ClassCastException: class java.lang.Double cannot be cast to class java.lang.Integer (java.lang.Double and java.lang.Integer are in module java.base of loader 'bootstrap')
	at .(#17:1)

Abbiamo già visto che il punto, in questo caso, è poter aggiungere e togliere elementi del tipo parametrico (avendo sia la garnzia della type safety che evitando l'uso del cast).

Ma gli array sono covarianti!

Si osservi che la situazione è ben diversa per gli array: è infatti vero che se S $\prec$ T, allora S[] $\prec$ T[].

Integer[] ai = new Integer[10];
Number[] an;

In questo caso, infatti, l'assegmaneto è possibile senza cast (per via della relazione di sottotipo)

an = ai;

Il fatto è che, per gli array, l'assegnamento a ao può essere controllato a run-time perché l'array conserva l'informazione circa il tipo dei suoi elementi (cosa che non accade per i tipi generici).

an[0] = 2.5;

---------------------------------------------------------------------------
java.lang.ArrayStoreException: java.lang.Double
	at .(#21:1)

L'eccezione ArrayStoreException è proprio il modo in cui la VM segnala (a runtime) che è impossibile assegnare un Double ad un elemento di ai (tramite l'alias an).

Attenzione: questo è ben lungi dall'essere un vantaggio! Infatti, il controllo a run-time (consentito dagli array) è molto meno desiderabile del controllo a compile-time (consentito dai generici), che assicura l'assenza di errori di tipo prima dell'esecuzione del programma.

Le wildcard

Per definire una gerarchia di sottotipo tra tipi generici è necessario introdurre un nuovo concetto: la wildcard (jolly). Se il parametro di tipo è sostituito da un ?, si parla di tipo generico con wildcard e vale che

• G<S> $\prec$ G<?> per ogni tipo S.

Il tipo G<?> può essere letto come "G di qualche tipo sconosciuto" e proprio per il fatto che non stabilisce il tipo parametrico, ha ben pochi usi. Ad esempio, definita una lista "di qualche tipo sconosciuto"

List<?> lw = li;

non è possibile aggiungervi alcun elemento (tranne null), perché non si sa di che tipo debbano essere gli elementi della lista

lw.add(1);

|   lw.add(1);
incompatible types: int cannot be converted to capture#2 of ?

per la stessa ragione non è possibile estrarne elementi di un tipo specifico (ma solo di tipo Object)

int x = lw.get(0);

|   int x = lw.get(0);
incompatible types: capture#3 of ? cannot be converted to int

I bound sulle wildcard

L'uso delle wildcard può essere reso più interessante specificando dei bound (limiti) sul tipo sconosciuto. In particolare, si possono specificare un bound che può essere:

• superiore, che si indica con la parola chiave extends e stabilisce che il "tipo sconosciuto" è un qualunque sottotipo di un certo tipo T. Si scrive quindi G<? extends T> e vale che

  • G<S> $\prec$ G<? extends T> se S $\prec$ T.

• inferiore, che si indica con la parola chiave super e stabilisce che il "tipo sconosciuto" è un qualunque supertipo di un certo tipo T. Si scrive quindi G<? super T> e vale che

  • G<S> $\prec$ G<? super T> se T $\prec$ S.

Si noti che i bound superiori sono covarianti, mentre quelli inferiori sono controvarianti (ossia l'ordine tra Ŧ e S si inverte).

Produttori e consumatori

Per comprendere l'uso delle wildcard con bound, consideriamo il caso dei produttori e consumatori di oggetti di un certo tipo T.

Un produttore è una classe che implementa l'interfaccia Supplier<T> il cui metodo get) può essere invocato per ottenre oggetti di tipo T. Ad esempio, un produttore in Integer è

import java.util.function.Supplier;

class NumeriPari implements Supplier<Integer> {
  int current = 2;
  @Override
  public Integer get() {
    int result = current;
    current += 2;
    return result;
  };
}

Supponiamo di voler scrivere un metodo che sommi i primi n numeri forniti da un produttore di Number

public static double sumFirstN(Supplier<Number> numbers, int n) {
  double sum = 0;
  for (int i = 0; i < n; i++) {
    sum += numbers.get().doubleValue();
  }
  return sum;
}

Purtroppo incappiamo nuovamente nel problema della non-covarianza dei generici

sumFirstN(new NumeriPari(), 5);

|   sumFirstN(new NumeriPari(), 5);
incompatible types: NumeriPari cannot be converted to java.util.function.Supplier<java.lang.Number>

Possiamo però usare la nuova arma delle wildcard con bound superiore

public static double sumFirstN(Supplier<? extends Number> numbers, int n) {
  double sum = 0;
  for (int i = 0; i < n; i++) {
    sum += numbers.get().doubleValue();
  }
  return sum;
}

in questo modo è garantito che il produttore produrrà al più oggetti di tipo Number (ossia oggetti di tipo Number o di suoi sottotipi). Di conseguenza, il metodo dobuleValue() è sempre definito sugli oggetti prodotti!

sumFirstN(new NumeriPari(), 5);

30.0

Passimo ora ai consumatori, che sono classi che implementano l'interfaccia Consumer<T> il cui metodo accept) è in grado di accettare oggetti di tipo T. Ad esempio, un consumatore di Number è

import java.util.function.Consumer;

class StampaQuadrato implements Consumer<Number> {
  @Override
  public void accept(Number n) {
    double val = n.doubleValue();
    System.out.println(val * val);
  }
}

Supponiamo di voler scrivere un metodo che offra i primi n numeri interi a un consumatore di Integer

void onFirstN(Consumer<Integer> consumer, int n) {
  for (int i = 0; i < n; i++) {
    consumer.accept(numbers.get());
  }
}

L'auspicio è che un consumatore di Number possa funzionare al posto di un consumatore di Integer

onFirstN(new StampaQuadrato(), 5);

|   onFirstN(new StampaQuadrato(), 5);
incompatible types: StampaQuadrato cannot be converted to java.util.function.Consumer<java.lang.Integer>

Ma di nuovo incappiamo nel problema della non-covarianza dei generici. Di nuovo possiamo usare le wildcard, questa volta con bound inferiore

void onFirstN(Consumer<? super Integer> consumer, int n) {
  for (int i = 0; i < n; i++) 
    consumer.accept(i);
}

per cui ora il nostro consumatore

onFirstN(new StampaQuadrato(), 5);

0.0

1.0

4.0

9.0

16.0

L'idea è che se un metodo accetta un produttore di T, allora può accettare anche un produttore di un sottotipo di T; d'altra parte, se un metodo accetta un consumatore di T, allora può accettare anche un consumatore di un supertipo di T. Questo principio è noto come il principio PECS (Producer Extends, Consumer Super).